Brief Announcement: Gathering Despite a Linear Number of Weakly Byzantine Agents

概要

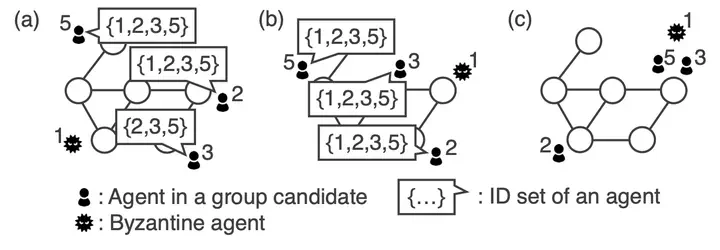
We study the gathering problem to make multiple agents initially scattered in arbitrary networks gather at a single node. There exist k agents with unique identifiers (IDs) in the network, and f of them are weakly Byzantine agents, which behave arbitrarily except for falsifying their IDs. The agents behave in synchronous rounds, and each node does not have any memory like a whiteboard. In the literature, there exists a gathering algorithm that tolerates any number of Byzantine agents, while the fastest gathering algorithm requires $\Omega(f^2)$ non-Byzantine agents.