Abstract
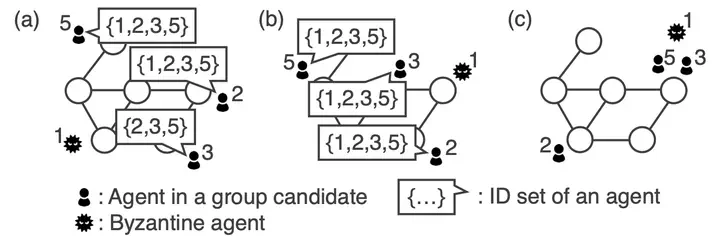
We study the gathering problem to make multiple agents initially scattered in arbitrary networks gather at a single node. There exist $k$ agents with unique identifiers (IDs) in the network, and $f$ of them are weakly Byzantine agents, which behave arbitrarily except falsifying their identifiers. The agents behave in synchronous rounds, and each node does not have any memory like a whiteboard. In the literature, two algorithms for solving the gathering problem have been proposed. The first algorithm assumes that the number $n$ of nodes is given to agents and achieves the gathering in $O(n^4· |Łambda_good|· X(n))$ rounds, where $|\Lambda_{good}|$ is the length of the largest ID among non-Byzantine agents, and $X(n)$ is the number of rounds required to explore any network composed of $n$ nodes. The second algorithm assumes that the upper bound $N$ of $n$ is given to agents and at least $4f^2+8f+4$ non-Byzantine agents exist, and achieves the gathering in $O((f+|\Lambda_{good}|)· X(N))$ rounds. Both the algorithms allow agents to start gathering at different times. The first algorithm can terminate agents simultaneously, while the second one not. In this paper, we seek an algorithm that solves the gathering problem efficiently with the intermediate number of non-Byzantine agents since there is a large gap between the numbers of non-Byzantine agents in the previous works. The resultant gathering algorithm works with at least $8f+8$ non-Byzantine agents when agents start the algorithm at the same time, agents may terminate at different times, and $N$ is given to agents. To reduce the number of agents, we propose a new technique to simulate a Byzantine consensus algorithm for synchronous message-passing systems on agent systems. The proposed algorithm achieves the gathering in $O(f·|\Lambda_{good}|·X(N))$ rounds. This algorithm is faster than the first existing algorithm and requires fewer non-Byzantine agents than the second existing algorithm if $n$ is given to agents, although the guarantees on simultaneous termination and startup delay are not the same.